多項式
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(2015年7月) |
数学における多項式(たこうしき、英: polynomial[注釈 1])は、定数および不定元(略式ではしばしば変数と呼ぶ)の和と積のみからなり、代数学の重要な対象となる数学的対象である。歴史的にも現代代数学の成立に大きな役割を果たした。また整式 (integral expression)[1] と呼ぶ流儀もある[注釈 2]。
不定元がひとつの多項式は、一元多項式あるいは一変数多項式 (univariate or univariable polynomial) と呼ばれ、その不定元を x とすれば、例えば "3x3 − 7x2 + 2x − 23" は多項式であり、和で結ばれた "3x3", "−7x2", "2x", "−23" の各々はこの多項式の項(こう、term)であると言う。すなわち、多項式とは「多数」の「項」を持つものである。一つの項だけからできている式を単項式 (monomial)、同様に二項式 (binomial)、三項式 (trinomial) などが、-nomial にラテン配分数詞を付けて呼ばれる。単項式の語が頻出であることに比べれば、二項式の語の使用はやや稀、三項式あるいはそれ以上の項数に対する語の使用はごく稀で一口に多項式として扱う傾向があり、それゆえ単項式のみ多項式から排他的に分類するものもある。
多項式同士の等式として与えられる方程式は多項式方程式と呼ばれ、特に有理数係数の場合において代数方程式という。多項式方程式は多項式函数の零点を記述するものである。
不定元がふたつならば二元 (bivariate), 三つならば三元 (trivariate) というように異なるアリティを持つ多元多項式が同様に定義できる。例えば "x3 + 2xyz2 − yz + 1" は三元 x, y, z の多項式である。算術あるいは初等代数学において、数の計算の抽象化として実数(あるいは必要に応じてより狭く有理数、整数、自然数)を代表する記号としての「文字」変数を伴う「文字式」[4]およびその計算を扱うが、それは大抵の場合多変数の多項式である。
本項では主として一元多項式を扱い、多元の場合にも多少触れるが、詳細は多元多項式の項へ譲る。
目次
1 基本用語
1.1 1変数の多項式
1.2 多変数の多項式
1.3 注意
1.3.1 多項式と整式
1.3.2 不定元と変数
1.3.3 記号 f と f(x)
2 多項式の演算
3 多項式関数
4 一般化
4.1 三角多項式
4.2 行列変数多項式
4.3 冪級数
4.4 ローラン多項式
4.5 ピュイズー多項式
4.6 指数多項式
4.7 非可換多項式
4.8 有理函数
5 関連項目
6 注
6.1 注釈
6.2 参考文献
7 関連文献
8 外部リンク
基本用語
1変数の多項式
不定元 x に関する(1変数の)多項式とは、

という形の式のことをいう。これを

とも書く。ただし、n は非負整数で、an, an − 1, …, a0 は数である。各々の akxk (k = 0, …, n) のことを項(より詳しくは k 次の項)とよび、ak をその項の係数とよぶ。特に、0次の項 a0 は定数項とよばれる。たとえば、多項式 3x3 − 7x2 + 2x − 23 の項とは 3x3, −7x2, 2x, −23 のことで、−7x2 の係数は −7 であり、またこの多項式の定数項は −23 である。
項を並べる順番は変更してよい。たとえば −7x2 − 23 + 2x + 3x3 は 3x3 − 7x2 + 2x − 23 と同じ多項式である。また、0 を係数とする項は省略してもよい。たとえば x2 + 0x − 1 と x2 − 1 は同じ多項式であり、0x2 + 4x − 2 と 4x − 2 も同じ多項式である。
−3x や 2x5 のような、唯一の項によって表される多項式のことを単項式とよぶ。また、数 a0 を多項式とみなすこともできる(定数多項式)。
定数多項式 0 を除くすべての多項式 f は、anxn + an − 1xn − 1 + … + a1x + a0(ただし an ≠ 0)という形に表すことができる。このように表したとき、n のことを多項式 f の次数とよび、また f は n 次多項式であるという。さらにこのとき、n 次の項 anxn は最高次の項ともよばれる。
定数多項式 a0 の次数は a0 = 0 の場合を除き 0 である。0 の次数は、定義しないか、あるいは −∞ と定めることが多い。
なお、多項式の係数としてはさまざまな範囲の数を用いることができる。どういった範囲の数を採用しているか明示するために、「実数を係数とする多項式」のような表現が用いられることがある。集合 K に属する数を係数とする多項式のことを「K 上の多項式」ともいう。係数の集合 K としては体または可換環を選ぶことが多いが、必ずしもそれらに限定されない。
多変数の多項式
不定元 x, y に関する2変数の多項式とは、たとえば −2x3y2 + x4 − 17xy2 − 4 のように、有限個の axkyl(k, l は非負整数、a は数)の和として表される式のことをいう。同様にして、任意の正整数 m について m 変数の多項式の概念を考えることができる。2変数以上の多項式は、一般に多変数の多項式とよばれる。
K を数の集合とする。m 個の不定元 x1, x2, …, xm に関する K 上の多項式 f は、m 個の非負整数の組全体の集合を ℤ≥0m で表すとき、ℤ≥0m のある有限部分集合 I を用いて

と表すことができる。ただし各 ak1k2…km は K の元である。同じことを、多重指数記法を用いて

と書くこともできる(ここで x = (x1, x2, …, xm) )。各々の ak1k2…kmx1k1x2k2…xmkm (多重指数記法では akxk)を多項式 f の項とよぶ。なお、1変数多項式の場合と同様に、0 を係数とする項は省略して書いてもよい。
m 変数の多項式 f を上記のように表したとき、項 ak1k2…kmx1k1x2k2…xmkm の次数とは、通常 k1 + k2 + … + km のことである。また、0 を係数とする項をすべて省略した形で f を書き表したときに、現れる項の次数のうち最大のものを f の次数とよぶ[5]。たとえば、(不定元 x, y に関する)多項式 −2x3y2 + x4 − 17xy2 − 4 の次数は 5 である。
注意
多項式と整式
「多項式」と「整式」は同じ意味で使われることもあるが、そうでない流儀もある。たとえば、「整式」を本記事でいう多項式の意味で用い、「多項式」は単項式でない整式の意味で用いる場合がある[要出典]。
また、現在の日本の中等教育課程では、本記事でいう多項式を「整式」とよび、「多項式」の語は副次的に用いる習慣がみられる。たとえば、中学校学習指導要領では「多項式」の語は「単項式」との対比においてのみ使われている[6]。高等学校学習指導要領には「多項式」は現れず、もっぱら「整式」の語が使われている[7]。
不定元と変数
多項式については、「不定元」と「変数」という二つの言葉は基本的に同じ意味で使われる。
不定元(変数)x に関する多項式 f があるとき、この f を多項式とみなす限りにおいては、x は単なる形式的な記号にすぎず、値を持ったりはしない。その意味で、x を「変数」とよぶのは不適切だと考えることもできる。一方で、f を多項式関数(後述)とみなした場合は x は変数となる。多項式と多項式関数は異なる概念ではあるけれども、両者には密接な関係があることから、多項式についても「不定元」でなく「変数」という言葉を用いる人も少なくない[要出典]。不定元も参照せよ。
記号 f と f(x)
多項式を記号で表す際の記法には、たとえば f と f(x) のように、不定元を表す文字を添えるものと添えないものがある。これらは両方とも広く用いられる。
多項式の演算
単位的可換環 R 上の多項式 f:=∑i=0maiXxi,g:=∑j=0lbjXj∈R[X]{textstyle f:=sum _{i=0}^{m}a_{i}Xx^{i},quad g:=sum _{j=0}^{l}b_{j}X^{j}in R[X]}![{textstyle f:=sum _{i=0}^{m}a_{i}Xx^{i},quad g:=sum _{j=0}^{l}b_{j}X^{j}in R[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5551b2e55595769c67ed9ff5e46d9cc4c396adbb)
- 相等
- f=g⟺[m=l∧ai=bi(∀i=0,…,m)]{displaystyle f=giff [m=lland a_{i}=b_{i}quad (forall i=0,dotsc ,m)]}
- 加法
- (∑i=0maiXi)+(∑j=0lbjXj)=∑k=0max(m,l)(ak+bk)Xk{displaystyle {Bigl (}sum _{i=0}^{m}a_{i}X^{i}{Bigr )}+{Bigl (}sum _{j=0}^{l}b_{j}X^{j}{Bigr )}=sum _{k=0}^{max(m,l)}(a_{k}+b_{k})X^{k}}
- 定数倍(スカラー倍)
- c⋅∑i=0maiXi=∑i=0mcaiXi{displaystyle ccdot sum _{i=0}^{m}a_{i}X^{i}=sum _{i=0}^{m}ca_{i}X^{i}}
- 乗法
- (∑i=0maiXi)(∑j=0lbjXj)=∑k=0m+l(∑i+j=kaibj)Xk{displaystyle {Bigl (}sum _{i=0}^{m}a_{i}X^{i}{Bigr )}{Bigl (}sum _{j=0}^{l}b_{j}X^{j}{Bigr )}=sum _{k=0}^{m+l}(sum _{i+j=k}a_{i}b_{j})X^{k}}
などの演算が定義される。多項式の加法およびスカラー倍は点ごとの演算、多項式の乗法は畳み込みあるいはコーシー積の一種として理解できる。特に積は、不定元 X と環 R の任意の元 a に対して、aX = Xa が成り立つと仮定して、分配法則が成り立つように定義されている(多項式の展開の項も参照)ので、R[X] は R 上の多元環になる。これを X を不定元とする R 係数の(一変数)多項式環あるいは簡単に、環 R 上の多項式環ともいう。R が単位的環であるなら、多項式環 R[X] も単位的環であり、R が可換なら多項式環 R[X] も可換環である。多項式環の単元群は係数環 R の単元群に等しい。
体 K 上の一変数多項式環 K[X] はユークリッド環であり、余りのある除法を定義することができる。
多項式関数
単位的可換環 K 上の多項式 f(X)=anXn+⋯+a0∈K[X]{textstyle f(X)=a_{n}X^{n}+cdots +a_{0}in K[X]}![{textstyle f(X)=a_{n}X^{n}+cdots +a_{0}in K[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00cbeedb5aba0718109f89a0c73bd09c275fe5de)

任意の f(X) ∈ K[X] を α ∈ K で評価することで与えられる評価写像 φα:K[X]→K;f(x)↦f(α){textstyle varphi _{alpha }colon K[X]to K;,f(x)mapsto f(alpha )}![{textstyle varphi _{alpha }colon K[X]to K;,f(x)mapsto f(alpha )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/157dbf47dfee16bd3c507a9acaa01dae64a203f3)
代入と評価に関して、より一般に以下のような普遍性が成り立つ:
- 代入準同型の普遍性
- 任意の単位的可換環 R, S とその間の単位的環準同型 h: R → S, および任意の α ∈ S が与えられたとき、単位的環準同型 ψh,α:R[X]→S{displaystyle psi _{h,alpha }colon R[X]to S}
が一意に存在して、ψh,α(X) = α かつ ψh,α(r) = h(r) (∀r ∈ R) を満たす。
この準同型 ψh,α を h の延長となる α の代入準同型とよぶ[8]。f(x)=anxn+⋯+a0{displaystyle f(x)=a_{n}x^{n}+cdots +a_{0}}

- 定義 (多項式函数)
- 与えられた多項式 f(X) = anXn + ⋯ + a0 ∈ K[X] に対し、f を各点 x ∈ K で評価することにより関数 が定まる。このような関数 f を総称して(K 上で定義された)多項式関数とよぶ。
f:K→K; x↦f(x)=anxn+an−1xn−1+⋯+a1x+a0{displaystyle fcolon Kto K; xmapsto f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+cdots +a_{1}x+a_{0}}
特に、多項式 f の次数 deg f が n であるとき、f の定める多項式関数は n 次関数と呼ばれる。
y = ax + b (a, b ∈ K, a ≠ 0) の形の多項式から定まる関数は一次関数と呼ばれる。
y = ax2 + bx + c (a, b, c ∈ K, a ≠ 0) の形の多項式から定まる関数は二次関数と呼ばれる。
- 注意 (多項式として等しいことと多項式函数として等しいこととは異なる)
- 係数の集合 K が実数体 R や複素数体 C などの無限体であれば、異なる多項式は異なる関数を定める。K が一般の可換環であるときはこの限りではない。例えば、有限体 F2 上多項式 X2 + X は零多項式 0 でないがこれの定める関数は零函数 0 である。無限体上、あるいは有限体上でも次数が体の位数よりも小さければ、このようなことは起きないことが知られている。
多項式の微分積分は以下の式が基本的である:
ddxxn=nxn−1,∫xndx=xn+1n+1+C.{displaystyle {frac {d}{dx}},x^{n}=nx^{n-1},quad int x^{n}dx={frac {x^{n+1}}{n+1}}+C.}(C{displaystyle C}
は積分定数)
これは解析学的に x を実数や複素数に値をとる変数と見る場合は、関数に対する微分・積分の定義から導かれる事実である。一方、代数学的にはこの式を定義として扱うことが多い(形式微分を参照)。
たとえば、多項式 X2 − 3X + 1 の微分(導多項式)は 2X − 3 となる。
- 複素変数の多項式関数はガウス平面の全域で正則な解析関数(整関数)である。
- 多項式が重根を持つことと、その多項式が自身の導多項式との間に共通の因数を持つこととが同値である。単根のみを持つ多項式は分離多項式と呼ばれる
一般化
多項式を一般化する筋道は少なくとも以下の二種類を考えることができる:
- 「多項式」や「多項式表示」という言葉を、単項式における不定元の冪積(特に一変数の単項式列 {1, x, x2, …})を特定の函数列で置き換えたり、あるいは不定元を行列などの数学的対象で置き換えた形と看做すことができる積和に対してしばしば用いる。
有理式や冪級数のような、多項式をその特別の場合として含むような対象。
三角多項式
実係数の三角多項式は n がいくつかの自然数を亙るときの三角函数 sin(nx), cos(nx) に関する有限線型結合 a0 + ∑N
n=1 an cos (nx) + ∑N
n=1 bn sin(nx) として表される実数値函数をいう[9]。これを「三角多項式」と呼ぶのは、多項式の単項式基底と函数列 sin(nx), cos(nx) を類似のものと看做してのアナロジーである。
また、複素係数の三角多項式とは、有限フーリエ級数(フーリエ多項式)のことを言う。これは eix を不定元と見て、その正負の冪によって張られる。
三角多項式の用例は広く、例えば周期函数の補間法に三角補間が用いられる。
行列変数多項式
行列多項式は行列変数の多項式である[10]。通常はスカラー値の多項式 P(x) = ∑n
i=0 aixi = a0 + a1x + a2x2 + ⋯ + anxn が与えられたとき、これを行列 A で評価した値というものを
- P(A)=∑i=0naiAi=a0I+a1A+a2A2+⋯+anAn{displaystyle P(A)=sum _{i=0}^{n}a_{i}A^{i}=a_{0}I+a_{1}A+a_{2}A^{2}+cdots +a_{n}A^{n}}
のこととして定義する。ここで、定数項は単位行列 I のスカラー倍に置き換わることに注意[11]:36。
行列多項式方程式は行列多項式の間の等式であって、考えている範囲の行列のうち特定のもののみがそれを満足するものを言う。同様に、考えている行列環 Mn(R) に属する任意の行列について成り立つ行列多項式の間の等式は行列多項式恒等式と呼ぶ。
冪級数
形式冪級数 ∑∞
n=0 anxn は多項式とよく似ているが、非零項が(可算)無限個あってもよい(つまり有限次とは限らない)点が異なる。ゆえに多項式と違って、一般には全ての項を陽に書き下すことは(無理数の小数表示が全て書ききれないことと同様の意味で)できない。しかし、各項に対する扱いや演算における項の操作ルールは多項式に対するものとまったく同じくすることができる。形式冪級数ではなく収束冪級数を考えることでも多項式を一般化することができるが、積は必ずしも収束するとは限らないので、環構造の埋め込みにはならないことに注意。形式冪級数は一般に次数に関して最大の非零項を持つとは限らないが、必ず最小の非零項を持つから、多項式の次数に対応する概念として形式冪級数の位数 (order) は最小の非零項の次数として定まる。
ローラン多項式
冪級数に対して、さらに有限個の負冪の項も許した一般化として形式ローラン級数が定義される。形式ローラン級数もまた最大の非零項を持つとは限らないが、必ず最小の非零項を持つ(が、略式的には両側無限和として ∑+∞
n=−∞ anxn のようにも書く)。
形式冪級数の特別の場合が多項式であったことの(形式)ローラン級数において対応する概念として、(形式)ローラン多項式は不定元の負冪の項を有限個含む多項式の類似物である。すなわち、ローラン多項式は正負の次数の項を含む有限和 ∑i=−NMaixi(N,M∈N){textstyle sum _{i=-N}^{M}a_{i}x^{i}quad (N,Min mathbb {N} )}
ピュイズー多項式
ピュイズー級数は冪級数に対して、分数冪を許すような一般化になっている。ピュイズー級数はアイザック・ニュートンが1676年に導入した[12]ものをビクトル・ピュイズーが再発見した[13]ためこの名がある。不定元 x に関する各ピュイズー級数は、適当な自然数 L に対する x1/L を不定元とするローラン級数
∑∞
n=l anxn/L として表される。ここで l は適当な整数であり、もちろん負であってもよい。代数閉体上のピュイズー級数体はそれ自身がまた代数閉体であり、またローラン級数体の代数閉包になる。
ピュイズー級数版の多項式として、ピュイズー多項式は有限和となっているようなピュイズー級数 ∑i=lmaixi/L(l≤m,l,m∈Z){textstyle sum _{i=l}^{m}a_{i}x^{i/L}quad (lleq m,;l,min mathbb {Z} )}
指数多項式
二変数多項式の第二変数を第一変数の指数函数で置き換えた P(x, ex) を指数多項式と呼ぶ。
非可換多項式
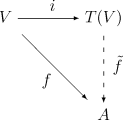
テンソル代数の普遍性
通常の多変数多項式環は、変数と係数および変数同士の可換性が仮定されている。この変数の間の可換性を仮定からはずすことで、非可換多項式環が定義される。可換性をはずしたために、非可換多項式を一般に書き表すのは困難であるが、非可換多項式環はテンソル代数として記述することができる。X = {x1, x2, ..., xn}を基底とする有限次元 K ベクトル空間あるいは可換環 K 上の階数有限な自由加群 V 上のテンソル代数 T(V) を
- T(V)=:K⟨x1,x2,…,xn⟩=K⟨X⟩{displaystyle T(V)=:Klangle x_{1},x_{2},ldots ,x_{n}rangle =Klangle mathbf {X} rangle }
などと記してK 上の非可換多項式環と呼ぶ。ここで術語「自由」(free) は、この環が必ずしも乗法が可換でないような多元環としての普遍性を持つということを意味している。K 上で有限生成な(非可換)環 A
- A=K⟨α1,α2,…,αn⟩:={∑lclαi1(l)αi2(l)⋯αikl(l)∣cl∈K,αij(l)∈{α1,…,αn}}{displaystyle A=Klangle alpha _{1},alpha _{2},ldots ,alpha _{n}rangle :=left{sum _{l}c_{l}alpha _{i_{1}}^{(l)}alpha _{i_{2}}^{(l)}cdots alpha _{i_{k_{l}}}^{(l)}mid c_{l}in K,alpha _{i_{j}}^{(l)}in {alpha _{1},ldots ,alpha _{n}}right}}
は K〈X〉 の代入による準同型像として得られる。つまり、適当な K 多元環の全射準同型で
- K⟨X⟩→A; f(x1,x2,…,xn)↦f(α1,α2,…,αn){displaystyle Klangle mathbf {X} rangle to A; f(x_{1},x_{2},ldots ,x_{n})mapsto f(alpha _{1},alpha _{2},ldots ,alpha _{n})}
なるものが必ず取れ、またしたがって A は K〈X〉 のある商多元環に同型である。この準同型の V への制限は V から A への K 線型写像であるが、逆に V から A への任意の K 線型写像はかならずこのような形の多元環の準同型に延長可能である。これはテンソル代数の普遍性と呼ばれる性質の一部である。
また、非可換多項式環 K〈x1, x2, …, xn〉 をテンソル代数とみるとき、対応する対称代数 S(V) (xy − yx の形の元全体で生成される両側イデアルで割った代数) は多項式環 K[x1, x2, …, xn] であり、多項式環が有限生成可換多元環に対する普遍性を持っていることに対応している。
有理函数
有理式は、二つの多項式 P, Q の商(代数的分数式)P(x)/Q(x) のことを言い、有理式として書き直すことのできる任意の代数式の定める函数を有理函数と呼ぶ。
多項式函数は変数に対する任意の代入に対して値が定義されるが、有理函数は分母が零にならないような変数の値に対してしか定義されない。
有理函数はローラン多項式を分母が不定元の冪であるような特別の場合として含む。
関連項目
多項式の因数分解: 可約/既約多項式, 素多項式, 原始多項式 (環論)
- 多項式補間
- 多項式列
- モニック多項式
- 多項式に関する主題一覧
多項式函数環: ベクトル空間上で定義される(座標を用いない仕方での)多項式函数からなる函数環
多項式変換 (方程式論): 多項式の求根において、もとの多項式の根が計算できるより容易に根の求まる函数や多項式へ変換すること。チルンハウス変換や分解方程式など。
注
注釈
^ 語義は、「多数」古希: poly- +「部分」 羅: -nomen あるいは 古希: νομός (nomós)
^ 整 (integer, entire) は「全体」あるいは「完全なもの」を意味する接頭辞で、この場合は代数式(特に根号を含まない有理式)が分母を持たないという意味である[2]。(本項で言うのと異なり)単項式や多項式を広義に単項代数式や多項代数式の意味で用いるならば、完全な単項式、完全な多項式という言い回しもある[3]
参考文献
^ ブリタニカ国際大百科事典 小項目事典『多項式』 - コトバンク
^ 日本大百科全書『整式』 - コトバンク
^ 長澤, 龜之助 (1907), 代数学精義, 成美堂, p. 16, https://books.google.com/books?id=0K5IgjUt7DcC
^ デジタル大辞泉『文字式』 - コトバンク
^ 日本数学会編 『岩波数学辞典』 岩波書店、2007年、第4版、893頁。ISBN 9784000803090。
^ 文部科学省 『中学校学習指導要領』、2008年3月。
^ 文部科学省 『高等学校学習指導要領』、2009年3月。
^ Knapp, Anthony W. (2007), Basic Algebra, Springer Science & Business Media, ISBN 9780817645298 Proposition 4.24 & Remarks
^ Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.
^ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 0-89871-681-0. Zbl 1170.15300.
^ Horn, Roger A.; Johnson, Charles R. (1990), Matrix Analysis, Cambridge University Press, ISBN 978-0521386326
^ Newton, Isaac (1960). “letter to Oldenburg dated 1676 Oct 24”. The correspondence of Isaac Newton. II. Cambridge University press. pp. 126–127. ISBN 0-521-08722-8
^ Puiseux, Victor Alexandre (1850年). “Recherches sur les fonctions algébriques”. J. Math. Pures Appl. 15: 365–480. http://sites.mathdoc.fr/JMPA/PDF/JMPA_1850_1_15_A24_0.pdf. , Puiseux, Victor Alexandre (1851年). “Nouvelles recherches sur les fonctions algébriques”. J. Math. Pures Appl. 16: 228–240. http://sites.mathdoc.fr/JMPA/PDF/JMPA_1851_1_16_A15_0.pdf.
関連文献
Barbeau, E.J. (2003). Polynomials. Springer. ISBN 978-0-387-40627-5. https://books.google.com/?id=CynRMm5qTmQC&printsec=frontcover.
Bronstein, Manuel, ed (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Springer. ISBN 978-3-540-27357-8. https://books.google.com/?id=aIlSmBV3yf8C&printsec=frontcover.
Cahen, Paul-Jean; Chabert, Jean-Luc (1997). Integer-Valued Polynomials. American Mathematical Society. ISBN 978-0-8218-0388-2. https://books.google.com/?id=AlAluH5is6AC&printsec=frontcover.
Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556, https://books.google.com/books?id=Fge-BwqhqIYC . This classical book covers most of the content of this article.
Leung, Kam-tim (1992). Polynomials and Equations. Hong Kong University Press. ISBN 9789622092716. https://books.google.com/?id=v5uXkwIUbC8C&printsec=frontcover.
- Mayr, K. Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen. Monatshefte für Mathematik und Physik vol. 45, (1937) pp. 280–313.
Prasolov, Victor V. (2005). Polynomials. Springer. ISBN 978-3-642-04012-2. https://books.google.com/?id=qIJPxdwSqlcC&printsec=frontcover.
Sethuraman, B.A. (1997). “Polynomials”. Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Springer. ISBN 978-0-387-94848-5. https://books.google.com/?id=yWnTIqmUOFgC&pg=PA119.
- Umemura, H. Solution of algebraic equations in terms of theta constants. In D. Mumford, Tata Lectures on Theta II, Progress in Mathematics 43, Birkhäuser, Boston, 1984.
- von Lindemann, F. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen. Nachrichten von der Königl. Gesellschaft der Wissenschaften, vol. 7, 1884. Polynomial solutions in terms of theta functions.
- von Lindemann, F. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen II. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, 1892 edition.
外部リンク
Hazewinkel, Michiel, ed. (2001), “Polynomial”, Encyclopaedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://eom.springer.de/p/p073690.htm
Euler's Investigations on the Roots of Equations, オリジナルの2011年5月22日時点によるアーカイブ。, https://web.archive.org/web/20110522161001/http://mathdl.maa.org/mathDL/46/?pa=content&sa=viewDocument&nodeId=640&pf=1
- Weisstein, Eric W. "Polynomial". MathWorld(英語). CS1 maint: Multiple names: authors list
Polynomial - PlanetMath.(英語)
| ||||||||||||||||

![{displaystyle f=giff [m=lland a_{i}=b_{i}quad (forall i=0,dotsc ,m)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f66e64f78ac542ecce9f54c9e81eacbda5c70047)







