極座標系
極座標系(きょくざひょうけい、英: polar coordinates system)とは、n 次元ユークリッド空間 Rn 上で定義され、1 個の動径 r と n − 1 個の偏角 θ1, …, θn−1 からなる座標系のことである。点 S(0, 0, x3, …,xn) を除く直交座標は、局所的に一意的な極座標に座標変換できるが、S においてはヤコビアン が 0 となってしまうから、一意的な極座標表現は不可能である。それは、S に於ける偏角が定義できないことからも明らかである。
目次
1 いろいろな極座標とその拡張
1.1 円座標
1.2 円柱座標
1.3 球座標
2 積分への応用
3 出典
4 関連項目
いろいろな極座標とその拡張
円座標
2 次元ユークリッド空間 R2 における極座標は円座標(circular coordinates)と呼ばれ、一つの動径座標と一つの角度座標からなる、最も単純な極座標である。rθ 平面、極座標平面(または平面極座標[1])ともいう。特異点は (r, θ) = (0, θ) 即ち、xy座標での原点 (x, y) = (0, 0) である。2 次元実ベクトル空間にも定義できることから、複素数体 C 上にも定義できる。この時、円座標を極形式と呼んだりもする。その場合、オイラーの公式を利用して z = reiθ と表す。円座標平面上で偏角を限定しなければ、これはxy平面上で円を描く。
円座標 (r,θ) から直交直線座標 (x,y) への変換は
{x=rcosθy=rsinθ{displaystyle {begin{cases}x=rcos theta \y=rsin theta \end{cases}}}
で与えられる。角度座標の範囲を −π < θ ≤ π とする場合の直交直線座標から円座標への変換は
{r=x2+y2θ=sgn(y)arccos(x/x2+y2){displaystyle {begin{cases}r={sqrt {x^{2}+y^{2}}}\theta =operatorname {sgn} (y)arccos(x/{sqrt {x^{2}+y^{2}}})\end{cases}}}
で与えられる。ここで sgn は符号関数である。原点 (x,y) = (0,0) において特異性があり、分母がゼロとなるため θ が定まらない。
円柱座標
円座標で (0, 0) を除く xy 平面上の全ての点を表現できるから、これに z 軸を加えれば、xyz 空間が表現できる。これを円柱座標(cylindrical coordinates)と言う。円柱座標空間上(rθz 空間上ともいう)で、θ, z を限定しなければ、これは xyz 空間上で円柱を描く。
また、円柱座標空間上の特異点は z 軸上の全ての点である。
円筒座標 (r,θ,z) から直交直線座標 (x,y,z) への変換は
{x=rcosθy=rsinθz=z{displaystyle {begin{cases}x=rcos theta \y=rsin theta \z=z\end{cases}}}
で与えられ、直交直線座標から円筒座標への変換は
{r=x2+y2θ=sgn(y)arccos(x/x2+y2)z=z{displaystyle {begin{cases}r={sqrt {x^{2}+y^{2}}}\theta =operatorname {sgn} (y)arccos(x/{sqrt {x^{2}+y^{2}}})\z=z\end{cases}}}
で与えられる。
球座標
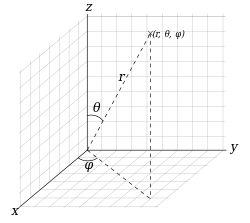
球座標による3次元ユークリッド空間内の点の表示
3 次元ユークリッド空間 R3 における極座標。球面座標(Spherical coordinates)とも呼ばれる。1 個の動径 r と 2 個の偏角 θ, φ によってなる(図を参照)。球座標において、動径を固定し、2 個の偏角を動かせば、xyz 空間上で球を描く。
球座標から直交直線座標への変換は
{x=rsinθcosϕy=rsinθsinϕz=rcosθ{displaystyle {begin{cases}x=rsin theta cos phi \y=rsin theta sin phi \z=rcos theta \end{cases}}}
で与えられ、直交直線座標から球座標への変換は
{r=x2+y2+z2θ=arccos(z/x2+y2+z2)ϕ=sgn(y)arccos(x/x2+y2){displaystyle {begin{cases}r={sqrt {x^{2}+y^{2}+z^{2}}}\theta =arccos(z/{sqrt {x^{2}+y^{2}+z^{2}}})\phi =operatorname {sgn} (y)arccos(x/{sqrt {x^{2}+y^{2}}})\end{cases}}}
で与えられる。z-軸上 (x,y) = (0,0) において特異性があり、分母がゼロとなるため φ が定まらない。原点においては θ も定まらない。
積分への応用
極座標平面での長方形は、直交座標に於ける扇形の一部となる。特に θ の長さが 2π であれば、直交座標においては円の一部となる。r を 0 から +∞ とすれば、この円は直交座標平面全体となる。従って、直交座標平面全体は、極座標平面に於ける長方形、r × θ = [0, ∞) × [0, 2π) に等しい。以上のことは広義二重積分に於いて有用である。なぜなら上記から、
- ∫−∞∞∫−∞∞f(x,y)dxdy=∫02π∫0∞f(rcosθ,rsinθ)rdrdθ{displaystyle int _{-infty }^{infty }int _{-infty }^{infty }f(x,y)dxdy=int _{0}^{2pi }int _{0}^{infty }f(rcos theta ,rsin theta )rdrdtheta }
が導けるからである。この公式は、例えば次のように用いられる。
- ∫−∞∞∫−∞∞e−(x2+y2)dxdy=∫02π∫0∞e−r2rdrdθ{displaystyle int _{-infty }^{infty }int _{-infty }^{infty }e^{-(x^{2}+y^{2})}dxdy=int _{0}^{2pi }int _{0}^{infty }e^{-r^{2}}rdrdtheta }
左辺の積分は、このままの状態で解くのは非常に困難だが、右辺の形にすれば、変数変換 r2 → r' によって、
- ∫02π∫0∞e−r2rdrdθ=12∫02π∫0∞e−r′dr′dθ{displaystyle int _{0}^{2pi }int _{0}^{infty }e^{-r^{2}}rdrdtheta ={frac {1}{2}}int _{0}^{2pi }int _{0}^{infty }e^{-r'}dr'dtheta }
とできるから、あとは通常の二重積分の方法に従って簡単に解け、答えは π となる。
出典
^ 小出昭一郎 『物理入門コース2 解析力学』 1-1〜1-3節、岩波書店、1983年
関連項目
- 直交座標系
- 斜交座標系









