図法幾何学
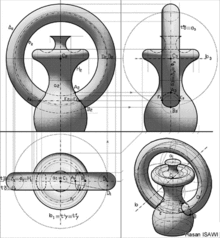
同じ3D物体で4つの異なる2D表現の例
図法幾何学(ずほうきかがく en:Descriptive_geometry)は、特定の一連手順で2次元や3次元物体の表現を可能にする幾何学手法。結果として得られる技術は工学、建築、デザインそしてアートにとって重要。[1] 図法幾何学の理論的基礎は平面幾何学的な投影によって提供される。この技術の最初期に著名な出版物は、アルブレヒト・デューラーによるニュールンベルグ、Linienで出版された『Underweysung der Messung mit der Zirckel und Richtscheyt』であった。また、ガスパール・モンジュは一般に「図法幾何学の父」とみなされている。彼は最初に軍事要塞の草案者として働いていた1765年に、幾何学的問題を解決するための技術として開発し発表した。[2]
モンジェの方法によって、仮想物体を3次元でモデル化することができるよう描画が可能となる。これにより想像上の物体のすべての幾何学的側面は、真のサイズ/スケールおよび形状で説明され、空間内の位置から見たときに撮像することができる。すべての画像は2次元表面上に表示される。
図法幾何学は想像上の物体から放射され、投影の仮想平面と直角に交差する架空の平行投影の画像生成技術を活用する。交点の累積ポイントは、所望の画像を生成する。
目次
1 手順
1.1 ヒューリスティック
1.2 一般的な解決策
2 関連項目
3 参考文献
手順
@media all and (max-width:720px){.mw-parser-output .tmulti>.thumbinner{width:100%!important;max-width:none!important}.mw-parser-output .tmulti .tsingle{float:none!important;max-width:none!important;width:100%!important;text-align:center}}
- オブジェクトの2つのイメージを相互に垂直な任意の方向に投影。各画像ビューは空間の3次元に対応し、2つの次元はフルスケールで互いに垂直な軸として表示され、1つは不可視(ポイントビュー)軸として画像空間(深度)に後退。2つの隣接する画像ビューのそれぞれは、空間の3つの次元のうちの1つのフルスケールビューを共有する。
- これらの画像のいずれかが、第3の投影されたビューの始点として機能することができる。第3のビューは、第4の投影を開始し、無限に開始することができる。これらの連続的な投影はそれぞれ、物体を異なる方向から見るために、90°回転する旋回した空間を表す。
- 新しい投影は、前のビューでポイントビューの次元として表示されるフルスケールの次元を使われる。このディメンションのフルスケール表示を実現して新しいビュー内で調整するには、前のビューを無視して、この次元がフルスケールで表示される2つ目の前のビューに進む必要がある。
- 新しい各ビューは、投影前の方向に垂直かつ無限の数ある方向のいずれかに投影することによって作成することができる(車軸のスポークの数ある方向をそれぞれ車軸の方向に垂直に想像する)。結果は、90°回転した物体の周りを巡回して各ステップから物体を見ることの1つである。新しいビューは、正投影レイアウト表示で追加ビューとして追加され、「ガラスボックスモデルの展開」として表示される。
このようにこの幾何学であれば、線の真の長さ(すなわち、フルサイズ、短縮されていないもの)と、四角形の頂点、ラインのポイントビュー(端面図)、平面の真の形状(すなわち、短縮されていないフルサイズの縮尺)、および平面のエッジビュー(すなわち、視線を有する平面のビューが平面の真の形状を生成するための視線と関連する視線に対して垂直である)で表される。
これらはしばしば、後続ビューの投影方向を決定するのに活用。90°の踏み込みプロセスによって、線のポイントビューから任意の方向に投影すると、その真の長さが得られ、ビュー; 真の長さのラインビューに平行方向で投影すると、そのポイントビューが得られ、プレーン上の任意のラインのポイントビューを投影すると、プレーンのエッジビューが得られる。平面のエッジビューに垂直な方向に投影すると、真の形状(縮尺通り)のビューが得られる。これらの様々な解は、固体幾何学の原理によってもたらされる工学的問題を解決するのに役立つことが求められるのである。
ヒューリスティック
画法幾何学を研究することには発見的価値がある。それは、視覚化と空間分析能力が促進されるだけでなく、解決のための幾何学的問題を最良に提示するため視覚方向を認識する直感的な能力を促進する。
代表的な例:
表示する最良の方向
- 最短のコネクタ(一般的な垂直)の位置を決定するために、一般的な位置にある2本のスキューライン(おそらくパイプ)
- 最短のコネクタが本格的に見えるような一般的な位置に2本のスキューライン(パイプ)
- 所与の平面に平行な最短のコネクタのような一般的な位置の2本のスキューラインは、フルスケールで(例えば、放射面から一定の距離で最短のコネクタの位置および寸法を決定するために)あたかも穴を覗いているかのように、垂直に穿孔された穴がフルスケールで見えるように(例えば、他の穿孔された穴との間隙を検査するために)
- 一般的な位置にある2本のスキューラインから等距離にある(安全な距離を確認するなど)
- ある点から平面までの最短距離(例えば、最も効果的な位置を特定するため)
- 湾曲したサーフェスを含む2つのサーフェス間の交線(たとえば、セクションの最も経済的なサイジングについては?)
- 2つの平面の間の角度の真のサイズ
正投影、逐次投影に類似したコンピュータモデリングビューを提示するための標準は、まだ採用されていない。そのような候補の1つを、下のイラストに示す。イラストの画像は、3次元のエンジニアリング・コンピュータグラフィックスを使用して作成された。
3次元のコンピュータモデリングは、「チューブの後ろに」仮想空間を生成し、この仮想空間内の任意の方向からモデルの任意のビューを生成することができる。これは、隣接する正射投影図を必要とせずに行うので、Descriptive Geometryの踏み越え手順を廃止したように見えうる。が、図学が3つの正法的または許容イメージの科学であるので、より多くの次元空間、平面上に、そしてそれがコンピュータモデリングの可能性を強化するために、必要不可欠な研究である。

画法幾何学を利用して2つのスキューライン間で最短のコネクタを見つける例 赤色、黄色、緑色のハイライトは、点Pの投影について同じ距離を示す。
一般的な解決策
問題に対しすべて可能な解決策を含む説明的な幾何学範囲の一連の解決策において単一の3次元オブジェクト(通常は円錐)で表され、その要素の方向は、無限の数の解のビューの任意のビュー(投影)の方向となる。
たとえば、一般的な位置(飛行中のロケットなど)の2つの不等長の斜め線が現れるような一般的な解を見つけるには:
- 等長
- 等しい長さと平行
- 等しい長さおよび垂直(例えば、少なくとも1つの理想的な標的化のため)
- 指定された比率の長さが等しい
- その他
これらの例では、それぞれの所望の特徴的な解についての一般的な解は円錐であり、その各要素は、無限の解のビューの1つを生成する。2つの円錐の間の2つの交点要素(円錐が接している場合には1つの要素)のいずれかの方向に突出し、上述のような2つ以上の特性が所望されている(解決策が存在する)場合、ソリューションビュー、円錐が交差しない場合、解は存在しない。以下の例は使用される記述的な幾何学的原理を示すために注釈が付けられている。TL =真の長さ。EV =エッジビュー。
また、以下の図1から3は、(1)画法幾何学、一般的解、および(2)同時に、正立法、多視点、レイアウト形式で潜在的に提示される標準解を示す。

図1 画法幾何 - 垂直に現れる斜め線

図2:画法幾何 - スキューラインは同じ長さで表示

図3:画法幾何 - 指定された長さの比率で斜め線が現れる
潜在的な標準は、2つの隣接する標準的な正法ビュー(ここでは、正面と上面)と標準の「折りたたみ線」を使用。ソリューションビューに到達するためには、標準的な2ステップのシーケンスで、オブジェクトの周りを90°回りに「回路的にステップ」する必要がないので(この場合、ソリューションビューに直接進むことができる)、この短いプロトコルがレイアウトのために説明される。1ステッププロトコルが2ステッププロトコルに置き換わる場合、「二重折り畳み」ラインが使用される。言い換えれば、二重線を横切ったとき、彼は90°の旋回をしていないが、正反対の回転は解決法のビューに直接向いている。大抵のエンジニアリングコンピュータグラフィックスパッケージは、ガラスボックスモデルの6つの主なビューと等角図を自動的に生成する
関連項目
- 射影幾何学
- 図形投影
投影図
正投影図
- 正射投影
軸測投影図
軸測投影
- 等角投影
- Dimetric投影
- 三角投影
- 直交射影
- 斜め投影
透視図
透視投影、パースペクティブ
- 作図
- 製図
- 製図論
- 設計図
参考文献
^ ジョセフMalkevitch(2003年4月)、「数学と芸術」[1]特集コラムアーカイブ、アメリカ数学会
^ イングリッドCarlbom、ジョセフPaciorek(1978年12月)"平面幾何学的投影および表示の変換"、ACMコンピューティング調査10 pp465-502


