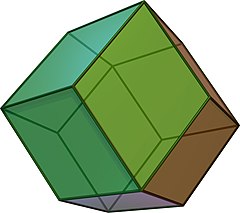
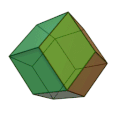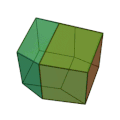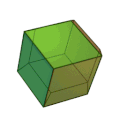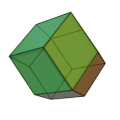
菱形十二面体
| 菱形十二面体 | |
|---|---|
  | |
| 種別 | カタランの立体、等面菱形多面体、平行多面体、十二面体 |
| 面数 | 12 |
| 面形状 | 菱形の一種  |
| 辺数 | 24 |
| 頂点数 | 14 |
| 対称群 | Oh |
| 双対多面体 | 立方八面体 |
| 特性 | 凸集合 |
 展開図 | |
菱形十二面体(りょうけいじゅうにめんたい、英: rhombic dodecahedron)とは、カタランの立体の一種で、立方八面体の双対多面体である。
この立体はゾーン多面体の一種であり[1]、その中でも、構成面が全て合同な菱形のため等面菱形多面体である。また、平行移動のみによって単独で空間充填できるので平行多面体でもあり[2]、その時のこの図形の配置は面心立方格子構造となる。
正六面体または正八面体の各面の中心を持ち上げ、隣り合う三角形同士が同一平面上となるようにした形、あるいは正四面体の各面と各辺の中心を持ち上げ、3つの四角形に分けたような形にもなっている。
柘榴石など、等軸晶系の鉱物はこのような形の結晶になることがある。
合同な菱形12枚で構成された多面体はもう1つ存在し、菱形十二面体第2種と呼ばれている。菱形十二面体の面は、対角線の比が1:√2(白銀比と呼ばれるものの一種)となっているが、菱形十二面体第2種のそれは黄金比となっている。こちらもゾーン多面体であり等面菱形多面体であるが、平行多面体ではない。
目次
1 性質
2 近縁な立体
3 関連項目
4 脚注
5 外部リンク
性質
 菱形十二面体サイコロ |
 菱形十二面体単独による空間充填 |
- 構成面となる菱形の形状
鈍角の角度: 約109.47°
鋭角の角度: 約70.53°[3]
- 長い対角線の長さ : 短い対角線の長さ : 辺の長さ = 2{displaystyle {sqrt {2}}}
:1:3{displaystyle {sqrt {3}}}
近縁な立体

正六面体
(ベースとなる形の1つ)

正八面体
(ベースとなる形の1つ)

正四面体
(ベースとなる形の1つ)

六方八面体
(各面の中心を持ち上げて変形)

凧形二十四面体
(各面の中心を更に持ち上げる)

五角二十四面体
(各頂点を、隣り合う頂点が逆方向となる形でねじる)

立方八面体と菱形十二面体による複合多面体
関連項目
菱形三十面体 - 菱形で構成されたもう一つのカタランの立体- 面心立方格子構造
脚注
^ George W. Hart (1999). “Zonohedrification”. The Mathematica Journal vol. 7 (no. 3). http://www.georgehart.com/zonohedra/zonohedrification.html.
^ Eric W. Weisstein (1999年5月25日). “Rhombic Dodecahedron”. 2018年8月29日閲覧。
^ Weisstein, E.W. (2002). CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. ISBN 9781420035223. https://books.google.com.tw/books?id=D_XKBQAAQBAJ.
外部リンク
- 太陽の馬~立方体の部品~
- Weisstein, Eric W. "Rhombic Dodecahedron". MathWorld(英語). CS1 maint: Multiple names: authors list
| ||||||||||||||||||||||||||||









