位相空間
この記事には参考文献や外部リンクの一覧が含まれていますが、脚注による参照が不十分であるため、情報源が依然不明確です。適切な位置に脚注を追加して、記事の信頼性向上にご協力ください。(2017年10月) |
数学における位相空間(いそうくうかん, 英語: topological space)とは、集合にある種の情報(位相、topology)を付け加えたもので、この情報により、連続性や収束性といった概念が定式化可能になる。
位相空間論は位相空間の諸性質を研究する数学の分野である。
目次
1 概要
1.1 位相空間と距離空間
1.2 応用分野
2 定義
2.1 開集合を使った特徴づけ
2.2 閉集合を使った特徴づけ
2.3 その他の特徴づけ
3 具体例
3.1 距離空間の位相構造
3.2 密着位相、離散位相、補有限位相、補可算位相
3.3 ザリスキ位相
4 位相空間に関する諸概念
4.1 近傍
4.2 内部、外部、境界
4.2.1 内部
4.2.2 外部
4.2.3 境界
4.3 閉包、稠密
4.4 性質
5 連続写像
5.1 一点での連続性
5.2 基本的性質
6 同相写像、位相不変性
6.1 位相不変量
7 収束
7.1 点列の収束
7.2 連続性との関係
7.3 距離空間における収束性と位相構造
7.4 一般化
7.5 一様連続と一様収束
8 位相同士の比較
9 位相空間の導出
9.1 逆像位相、部分位相、始位相、直積位相
9.1.1 逆像位相
9.1.2 部分位相
9.1.3 始位相
9.1.4 直積位相
9.2 像位相、商位相、終位相、直和位相
9.2.1 像位相
9.2.2 商位相
9.2.3 終位相
9.2.4 直和位相
9.3 ヴィートリス位相、コンパクト開位相
9.3.1 ヴィートリス位相
9.3.2 コンパクト開位相
10 基本近傍系
11 位相の生成、開基、準開基
11.1 準開基
11.2 開基
11.3 開基の具体例
11.4 開基の特徴づけ
11.5 準開基の特徴づけ
12 位相的性質
12.1 分離公理
12.2 連結性
12.3 コンパクト性
12.4 可算公理と可分
12.4.1 性質と例
12.5 距離化可能性
12.6 この他の諸性質
13 発展的なトピック
13.1 連続体論
13.2 完全不連結性とカントール空間
13.3 ベール空間
13.4 集合論的位相空間論
13.5 位相ゲーム
13.6 位相代数的構造
13.7 位相順序構造
14 歴史
15 参考文献
16 脚注
17 関連項目
18 外部リンク
概要
位相空間は、前述のように集合にある種の情報(位相)を付け加えたもので、この情報により、例えば以下の概念が定義可能となる
- 部分集合の内部、外部、境界
- 点の近傍
- 点列の収束
- 連結性
- 位相空間から位相空間への写像の連続性
- 開集合、閉集合、閉包
これらの概念の多くは元々距離空間のような幾何学的な対象に対して定義されたものだが、位相空間としての性質を満たしさえすれば、解析学や代数学の研究対象に対してもこれらの概念を定義できることに位相空間の概念の利点の一つがある。これにより、位相空間の概念は、幾何学はもちろん解析学や代数学でも応用されており、位相空間論はこうした数学の諸分野の研究の基礎を与える。別の言い方をすると、位相空間の概念の利点の一つは、解析学や代数学などの研究対象に幾何学的な直観を与えることにある。
このような観点からみたとき、位相空間論の目標の一つは、ユークリッド空間など幾何学の対象に対して成り立つ諸性質を解析学などにも一般化することにある。従って特に学部レベルにおいては、位相空間論で考える性質の多くは、ユークリッド空間などの幾何学的な対象では自明に成り立つ(例えば各種分離公理や可算公理)。
こうした幾何学的な性質をいかに抽象化してより一般の空間へと拡張するかが位相空間論では問われる。位相空間の概念自身は非常に弱く、かつ抽象的に定義されているため、数学の様々な分野で広く応用可能である。しかしその分個別の用途では必要な性質が満たされないこともあり、例えば位相空間では必ずしも点列の収束の一意性は保証されない。そこで必要に応じて、位相空間にプラスアルファの性質を付け加えたものが研究対象になることも多い。前述した収束の一意性は、位相空間に「ハウスドルフ性」という性質を加えると成立する。学部レベルの位相空間論の目標の一つは、こうしたプラスアルファの性質の代表的なものを学ぶ事にある。
位相空間と距離空間
位相空間となる代表的な空間としては、ユークリッド空間をはじめとした距離空間がある。(なお、距離空間は必ず位相空間になるが、逆は必ずしも正しくない)。
しかしユークリッド空間など多くの空間では、位相空間としての構造は距離空間としての構造よりも遙かに弱いものになっており、距離空間としては異なっても位相空間としては同一の空間になることもある。
例えばユークリッド空間をゴム膜のように連続変形したものは、元のユークリッド空間とは距離空間としては異なるが、位相空間としては同一である。実際、点列が収束するか否かという位相空間の代表的な性質は、ユークリッド空間をゴム膜のように連続変形しても不変である。
この例でもわかるように、連続性や収束性といった概念を考えるときには、距離空間の概念は柔軟性に欠けるところがあり、位相空間というより弱い概念を考える積極的動機の一つとなる。
他にも例えば多様体を定義する際には複数の距離空間(ユークリッド空間の開集合)を連続写像で「張り合わせる」(商空間)が、張り合わせに際して元の空間の距離構造を壊してしまうので、元の空間を距離空間とみなすより、位相空間とみなす方が自然である。
応用分野
位相空間の概念の代表的な応用分野に位相幾何学がある。これは曲面をはじめとした幾何学的な空間(主に有限次元の多様体や単体的複体)の位相空間としての性質を探る分野である。前述のようにゴム膜のように連続変形しても位相空間としての構造は変わらないので、球面と楕球は同じ空間であるが、トーラスは球面とは異なる位相空間である事が知られている。位相幾何学では、位相空間としての構造に着目して空間を分類したり、分類に必要な不変量(位相不変量)を定義したりする。

コーヒーカップからドーナツ(トーラス)への連続変形(同相写像の一種)とその逆
位相空間の概念は代数学や解析学でも有益である。例えば無限次元ベクトル空間を扱う関数解析学の理論を見通しよく展開するにはベクトル空間に位相を入れて位相空間の一般論を用いることが必須であるし(位相線型空間)、代数幾何学で用いられるザリスキ位相は、通常、距離から定めることのできないような位相である。
また、位相空間としての構造はその上で定義された様々な概念の制約条件として登場することがある。例えばリーマン面上の有理型関数のなす空間の次元は、リーマン面の位相構造によって制限を受ける(リーマン・ロッホの定理)。また三次元以上の二つの閉じた双曲多様体が距離空間として同型である必要十分条件は、位相空間として同型な事である(モストウの剛性定理)。
定義
位相空間にはいくつかの同値な定義があるが、本項ではまず、開集合を使った定義を述べる。
開集合を使った特徴づけ
位相空間を定式化する為に必要となる「開集合」という概念は、直観的には位相空間の「縁を含まない」、「開いた」部分集合である。
ただし上ではわかりやすさを優先して「縁を含まない」、「開いた」という言葉を使ったが、これらの言葉を厳密に定義しようとすると位相空間の概念が必要になるので、これらを使って開集合を定義するのは循環論法になってしまう。また、ここでいう「縁」(=境界)は通常の直観と乖離している場合もあり、例えば実数直線上の有理数の集合の境界は実数全体である。
そこで位相空間の定義では、「縁を含まない」とか「開いた」といった概念に頼ることなく、非常に抽象的な方法で開集合の概念を定式化する。
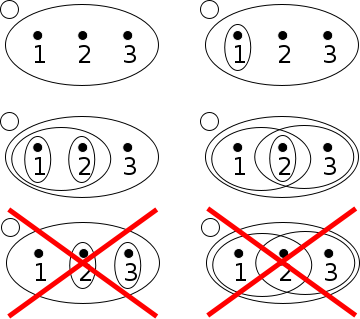
位相空間を定式化するのに必要なのは、どれが開集合であるのかを弁別するために開集合全体の集合O{displaystyle {mathcal {O}}}

位相空間の厳密な定義は以下のようになる。
Xを集合とし、O{displaystyle {mathcal {O}}}

O{displaystyle {mathcal {O}}}



- ∅,X∈O{displaystyle emptyset ,Xin {mathcal {O}}}
- ∀O1,O2∈O : O1∩O2∈O{displaystyle forall O_{1},O_{2}in {mathcal {O}}~~:~~O_{1}cap O_{2}in {mathcal {O}}}
- ∀{Oλ}λ∈Λ⊂O : ⋃λ∈ΛOλ∈O{displaystyle forall {O_{lambda }}_{lambda in Lambda }subset {mathcal {O}}~~:~~bigcup _{lambda in Lambda }O_{lambda }in {mathcal {O}}}
これらの性質の直観的意味は下記の通りである
空集合と全体集合は開集合である。- 2つの開集合の共通部分は開集合である。(よって(零個を除く)有限個の開集合の共通部分は開集合 となるが、無限個の共通部分は開集合とは限らない)
- 任意の個数(有限でも無限でもよい)の開集合の和集合は開集合である。
開集合系O{displaystyle {mathcal {O}}}

紛れがなければ開集合系O{displaystyle {mathcal {O}}}
また位相空間X の元を点と呼ぶ。
なお、「(集合算に関する)空積および空和を認める」という規約を置いた上で、上記条件 1. を削り、条件 2. を 2.’「有限個の開集合の共通部分は開集合」に変えることも出来る。即ちこのような規約に則れば、残りの条件 2.’、3. より 1. が導かれる(cf. 交叉 (数学)#空なる交叉)。松坂は前者、Bourbaki は後者の立場である[1]。
閉集合を使った特徴づけ
開集合のX における補集合の事を閉集合と呼ぶ。開集合が直観的には「縁を含まない」、「開いた」集合だったのに対し、閉集合は直観的には「縁を含んだ」、「閉じた」集合である。
閉集合全体の集合
- F={F⊂X∣Fc∈O}{displaystyle {mathcal {F}}={Fsubset Xmid F^{c}in {mathcal {O}}}}
の事を位相空間X の閉集合系と呼ぶ。
前述した開集合系の定める公理にド・モルガンの法則を適用することにより、F{displaystyle {mathcal {F}}}
- ∅,X∈F{displaystyle emptyset ,Xin {mathcal {F}}}
- ∀F1,F2∈F : F1∪F2∈F{displaystyle forall F_{1},F_{2}in {mathcal {F}}~~:~~F_{1}cup F_{2}in {mathcal {F}}}
- ∀{Fλ}λ∈Λ⊂F : ⋂λ∈ΛFλ∈F{displaystyle forall {F_{lambda }}_{lambda in Lambda }subset {mathcal {F}}~~:~~bigcap _{lambda in Lambda }F_{lambda }in {mathcal {F}}}
本項ではこれまで、開集合系を使って位相空間を定義し、開集合の補集合として閉集合を定義した。
しかし逆に上述の性質を満たたす閉集合系F{displaystyle {mathcal {F}}}
X の開集合でも閉集合でもあるような部分集合は X の開かつ閉集合と呼ばれる(定義から明らかに ∅{displaystyle emptyset }
その他の特徴づけ
具体例
距離空間の位相構造
距離空間(X ,d )は、以下のようにして位相空間とみなせる。実数 r > 0 と x ∈ X に対し、
- Br(x):={y∈X∣d(x,y)<r}{displaystyle B_{r}(x):={yin Xmid d(x,y)<r}}
とし、
O ⊂ X が以下の性質を満たすとき、O は X の開集合であるという
- ∀x∈O∃r>0 : Br(x)⊂O{displaystyle forall xin Oexists r>0~~:~~B_{r}(x)subset O}
以上のように定義された開集合全体の集合をO{displaystyle {mathcal {O}}}

以下、単に「距離空間の位相構造」と言ったら、上述の位相構造を指すものとする。
密着位相、離散位相、補有限位相、補可算位相
X を集合とするとき、空集合∅{displaystyle emptyset }

また、X の任意の部分集合を開集合とする開集合系O=P(X){displaystyle {mathcal {O}}={mathfrak {P}}(X)}
密着位相と離散位相はいわば「両極端」の人工的な位相構造に過ぎないが、これらの位相構造は、位相に関する命題の反例として用いられる事がある。
またこれらの位相構造は、任意の集合上に位相構造を定義できる事を意味している。
任意の無限集合 X には、さらに補有限位相という位相も入れることができる。これはXの有限集合部分全体の集合を閉集合系とみなす位相である。なおX が有限集合である場合も原理的には補有限位相を定義できるが、この場合は離散位相と一致する。
同様に任意の非可算集合 Xには補可算位相を入れることができ、これはXの可算集合部分全体の集合を閉集合系とみなす位相である。
ザリスキ位相
分離性を満たさない位相空間で代数学・数論的に重要なものとして素スペクトルや極大スペクトルが挙げられる。これは単位的な可換環に対して自然に定義されるもので、環 R のスペクトル SpecR{displaystyle operatorname {Spec} mathbf {R} }


特に整数のなす環 Z の極大スペクトルは素数全体の集合 P = {2, 3, 5, 7, ...} と同一視でき、その閉集合は P の任意の有限部分集合および P 全体としてあたえられる。
位相空間に関する諸概念
近傍
(X,O){displaystyle (X,{mathcal {O}})}
X の部分集合A が以下を満たすとき、A はx の 近傍(きんぼう, 英: neighborhood)であるという
- ある開集合O ⊂ X が存在し、x ∈ O ⊂ A
x の近傍でしかも開集合であるものを開近傍といい、x の近傍でしかも閉集合であるものを閉近傍という。
開集合O がx の開近傍である必要十分条件は、x ∈ O となることである。
内部、外部、境界
内部
(X,O){displaystyle (X,{mathcal {O}})}
このとき、x ∈ X がA の内点であるとは、A がx の近傍である事を指し、A の内点全体の集合をA の内部(ないぶ, 英: interior)または開核という。
定義から明らかなように、x ∈ X がA の内点である必要十分条件は、以下が満たされることである
- ある開集合O ⊂ X が存在し、x ∈ O ⊂ A
A の内部を
- A∘, IntA{displaystyle A^{circ }, operatorname {Int} A}
などで表す。
外部
一方、A c の内点をA の外点と呼び、A の外点全体の集合をAの外部(がいぶ, 英: exterior)という。
定義から明らかなように、x ∈ X がA の外点である必要十分条件は、以下が満たされることである
- ある開集合O ⊂ X が存在し、x ∈ O ⊂ A c
A の外部を以下のように表す
- Ae, ExtA{displaystyle A^{e}, operatorname {Ext} A}
境界
A の内点でも外点でもない 点x ∈ X をA の境界点といい、境界点全体の集合をA の境界(きょうかい, 英: frontier)という。
定義から明らかなように、x ∈ X がA の境界点である必要十分条件は、以下が満たされることである
x の任意の開近傍O ⊂ X に対し、A∪O≠∅{displaystyle Acup Oneq emptyset }かつ Ac∪O≠∅{displaystyle A^{c}cup Oneq emptyset }
A の境界を
- FrA, BdA, ∂A{displaystyle operatorname {Fr} A, operatorname {Bd} A, partial A}
などで表す。なお、「∂A{displaystyle partial A}
閉包、稠密
- A¯:=A∘∪Fr(A){displaystyle {overline {A}}:=A^{circ }cup operatorname {Fr} (A)}
をA の閉包(へいほう, 英: closure)と呼び、A の閉包に属する点を A の触点と呼ぶ。
A の閉包は、
- Cl(A), A−{displaystyle operatorname {Cl} (A), A^{-}}
といった記号で表される事もある。
定義から明らかなように、x がA の触点である事は、x がA の外点ではない事と同値である。よって x がA の触点である事は、以下のように言い換えられる
xの任意の開近傍O に対し、A∩O≠∅{displaystyle Acap Oneq emptyset }
閉包の概念は、以下の性質を満たす(クラトフスキーの公理)。
- A⊂A¯{displaystyle Asubset {overline {A}}}
- A¯¯=A¯{displaystyle {overline {overline {A}}}={overline {A}}}
- A∪B¯=A¯∪B¯{displaystyle {overline {Acup B}}={overline {A}}cup {overline {B}}}
- ∅¯=∅{displaystyle {overline {emptyset }}=emptyset }
- A⊂A¯{displaystyle Asubset {overline {A}}}
本項ではこれまで、開集合系を使って位相空間を定義し、これをベースに閉包を定義した。
しかし逆に上述の性質を満たたす閉包作用素を使って位相空間を定義し、これを使って開集合と定義する事も可能である。
A が X の稠密な部分集合であるとは、A の閉包が X に一致することである。つまり、X の任意の点の任意の近傍が、A と交わることである。可算な稠密部分集合をもつ位相空間は可分であるという。
性質
以上の概念について次が成立する。
- 内部、境界、外部は、全空間X を排他的に分割する
- A∘⊔Fr(A)⊔Ae=X{displaystyle A^{circ }sqcup operatorname {Fr} (A)sqcup A^{e}=X}
- 外部、内部は開集合で、境界は閉集合である。
- 閉包 A¯{displaystyle {overline {A}}}
は A を含む最小の閉集合である。
- 内部 A∘{displaystyle A^{circ }}
は A に含まれる最大の開集合である。
- A∘⊂A⊂A¯, A∘ =(Ac¯)c, FrA=A¯∩Ac¯.{displaystyle A^{circ }subset Asubset {overline {A}}, A^{circ } =({overline {A^{c}}})^{c}, operatorname {Fr} A={overline {A}}cap {overline {A^{c}}}.}
連続写像
位相空間の概念を考える利点の一つに、連続性の概念が非常に簡潔に定式化できる事が挙げられる。
(X,OX){displaystyle (X,{mathcal {O}}_{X})}

- ∀O∈OY : f−1(O)∈OX{displaystyle forall Oin {mathcal {O}}_{Y}~~:~~f^{-1}(O)in {mathcal {O}}_{X}}
すなわち、Y の開集合のf による逆像が必ず開集合になるとき、f は連続であるという。
以下が成立する
X、Y が距離空間である場合、前述した連続性の定義はイプシロン・デルタ論法による連続性の定義と同値である。
一点での連続性
(X,OX){displaystyle (X,{mathcal {O}}_{X})}

- ∀V ⊂ Y : V が f(x) の近傍⇒ f−1(V) はx の近傍
以下が成立する
- 全ての点x ∈X でf が連続⇔f は連続
X 、Y が距離空間のとき、f がイプシロン・デルタ論法による定義において点x で連続⇔f は上述の意味で点x ∈X で連続
近傍の定義より、写像 f が点x で連続であることは次のように言い換えられる。
f(x) の任意の近傍 V に対して、x の近傍 U が存在して、f(U)⊂V{displaystyle f(U)subset V}となる
よって位相空間における一点での連続性の概念は、イプシロン・デルタ論法による一点での連続性の定義を自然に拡張したものになっている。
基本的性質
X、Y、Z を位相空間として、f : X → Y、g{displaystyle g}
Y の任意の閉集合 F に対して、逆像 f−1(F){displaystyle f^{-1}(F)}は X の閉集合である。
合成関数 g∘f{displaystyle gcirc f}: X → Z は連続である。
同相写像、位相不変性
(X,OX){displaystyle (X,{mathcal {O}}_{X})}

また、X、Y 間に同相写像が存在するとき、(X,OX){displaystyle (X,{mathcal {O}}_{X})}

位相同型性は、位相空間のクラスにおける同値関係であることを簡単に確認できる。
位相空間論や、その応用分野である位相幾何学では、「位相同型で不変」(位相不変性)な性質(位相的性質)を探ったり、そうした性質により、空間を分類する。
位相不変量
位相不変な性質の中には位相不変量と呼ばれる、位相空間の性質によって決まる「量」がある。
χが「位相不変量」であるとは、以下の性質を満たすことを言う
X と Y が位相同型⇒χ(X )=χ(Y )
これの対偶をとると、
- χ(X )≠χ(Y )⇒ X と Y が位相同型でない
したがって位相不変量に着目することで、二つの空間を位相的に分類することができる。
簡単な位相不変量として、位相空間の「連結成分数」がある。本項では、連結成分数の厳密な定義は割愛するが、直観的にはその名の通り、「繋がっている部分の数」である。以下のX では連結成分数が1なのに対し、Y では連結成分数が2である。従ってX と Y は位相同型ではない。
X = [0,1]
Y = [0,1]∪[2,3]
位相不変量は、位相空間論の応用分野である位相幾何学で主要な役割を果たし、特にホモロジー群やホモトピー群のような代数的な不変量は代数的位相幾何学の研究対象である。
収束
点列の収束
(X,O){displaystyle (X,{mathcal {O}})}

以下が満たされるとき、{xn}n=1∞{displaystyle scriptstyle {x_{n}}_{n=1}^{infty }}
- ∀U (x の近傍) ∃n0∀n>n0 : xn∈U{displaystyle exists n_{0}forall n>n_{0}~~:~~x_{n}in U}
この収束の定義は、実数列の収束の自然な拡張となっている。
一般の位相空間では収束の一意性が成り立たないが、収束の一意性が成り立つ十分条件として、ハウスドルフ性がある。
連続性との関係
収束の概念は、連続性の概念で言い換えることができる。
自然数と無限大の集合N∪{∞}{displaystyle mathbb {N} cup {infty }}
- (a,∞]={x∈N∣x>a}∪{∞}{displaystyle (a,infty ]={xin mathbb {N} mid x>a}cup {infty }}
の形をした集合を開集合とみなす位相(右順序位相)入れることで、N∪{∞}{displaystyle mathbb {N} cup {infty }}
このとき、位相空間(X,O){displaystyle (X,{mathcal {O}})}

- N∪{∞}→X, n↦{xn if n∈Nx if n=∞{displaystyle mathbb {N} cup {infty }to X,~~nmapsto {begin{cases}x_{n}&{text{ if }}nin mathbb {N} \x&{text{ if }}n=infty end{cases}}}
が∞で連続になる事である。
距離空間における収束性と位相構造
距離空間の位相的な性質を点列の収束で特徴づけることができる。
例えば、
F が閉集合⇔∀n : xn∈F{displaystyle forall n~~:~~x_{n}in F}を満たす任意の収束点列の収束先は必ず F に属する
- 距離空間から距離空間への関数 f が点 x で連続⇔xn→x{displaystyle x_{n}to x}
となる点列は必ずf(xn)→f(x){displaystyle f(x_{n})to f(x)}
を満たす
一般化
距離空間の場合、点列の収束の概念を用いることで連続性や閉集合といった基礎的概念を特徴づけることができたが、一般の位相空間ではそのような事はできない。(これが可能な空間を列型空間という)。
これは点列という概念が、自然数という限定的な添え字しか許さないことや、点の列だけで集合の列を考慮していない事などが原因である。
しかし、そうした側面に対して点列の概念を一般化したものである有向点族やフィルターの概念を用いれば、前述した基礎的概念をこれらの収束性で特徴づけることができる。
これらの収束性を考える利点はもうひとつあり、点列の収束性では必要性しかいえない命題が、これらの収束性を用いれば、必要十分性が言えるときがある。
例えば点列の収束の一意性は、前述したハウスドルフ性の必要条件に過ぎないが、有向点族の収束の一意性はハウスドルフ性の必要十分条件となる。
一様連続と一様収束
これまで説明してきたように、連続性と収束性は、位相空間で定義可能な代表的な性質である。
しかしこれらを強めた概念である一様連続性と一様収束性は、位相のみをベースにして定義する事はできない。
これらの概念は、距離空間と位相空間の中間の強さを持つ概念である一様空間で定義可能である。
位相同士の比較
集合X 上で定義された2つの位相空間(X,O1){displaystyle (X,{mathcal {O}}_{1})}

以下が満たされるとき、O1{displaystyle {mathcal {O}}_{1}}

- O1⊂O2{displaystyle {mathcal {O}}_{1}subset {mathcal {O}}_{2}}
これはすなわち、(X,O1){displaystyle (X,{mathcal {O}}_{1})}

O1{displaystyle {mathcal {O}}_{1}}



O1{displaystyle {mathcal {O}}_{1}}

- id : (X,O2)→(X,O1), x↦x{displaystyle operatorname {id} ~:~(X,{mathcal {O}}_{2})to (X,{mathcal {O}}_{1}), xmapsto x}
が連続な事である。
粗い/細かいを位相の間の順序関係とみなすと、X 上の位相の集合
{O∣(X,O){displaystyle {{mathcal {O}}mid (X,{mathcal {O}})}は位相空間}{displaystyle }}
は順序集合になる。この順序集合は完備束であり、最も粗い位相は密着位相、最も細かい位相は離散位相である。
位相空間の導出
すでにある位相空間を加工して、別の位相空間を作る方法を述べる。
位相空間を加工する上で基本となるのは、「逆像位相」と「像位相」の概念、おそびそれらの拡張概念である「始位相」と「終位相」である。
逆像位相と像位相、始位相と終位相は互いに双対の関係にあり、写像の向きを逆にすることでもう片方の概念を定式化できる。
逆像位相、部分位相、始位相、直積位相
逆像位相
(X,O){displaystyle (X,{mathcal {O}})}

- f : Z→X{displaystyle f~:~Zto X}
を写像とする。このとき、
- f∗(O):={f−1(O)∣O∈O}{displaystyle f^{*}({mathcal {O}}):={f^{-1}(O)mid Oin {mathcal {O}}}}
とすると、(Z,f∗(O)){displaystyle (Z,f^{*}({mathcal {O}}))}

次の事実が知られている
- 逆像位相は、写像f : Z→X{displaystyle f~:~Zto X}
を連続とする最弱の位相である
部分位相
(X,O){displaystyle (X,{mathcal {O}})}
このとき、包含写像
- ι : A↪X, x↦x{displaystyle iota ~:~Ahookrightarrow X, xmapsto x}
による逆像位相をX によるA の部分位相といい、A に部分位相を入れたものを(X,O){displaystyle (X,{mathcal {O}})}
部分位相の開集合系は、以下のように書くことができる
- {O∩A∣O∈O}{displaystyle {Ocap Amid Oin {mathcal {O}}}}
始位相
逆像位相の概念は、以下のように一般化できる。
Z{displaystyle Z}

- fλ : Z→Xλ{displaystyle f_{lambda }~:~Zto X_{lambda }}
を考える。
このとき、全ての{fλ}λ∈Λ{displaystyle {f_{lambda }}_{lambda in Lambda }}
始位相は、
- ⋃λ∈Λfλ∗(Oλ){displaystyle bigcup _{lambda in Lambda }f_{lambda }{}^{*}({mathcal {O}}_{lambda })}
から生成される位相と一致する。
直積位相
{(Xλ,Oλ)}λ∈Λ{displaystyle {(X_{lambda },{mathcal {O}}_{lambda })}_{lambda in Lambda }}


- πλ : ∏τ∈ΛXτ→Xλ{displaystyle pi _{lambda }~:~prod _{tau in Lambda }X_{tau }to X_{lambda }}
の族{πλ}λ∈Λ{displaystyle {pi _{lambda }}_{lambda in Lambda }}


直積位相は
{∏λ∈ΛOλ | Oλ∈Oλ{displaystyle {Bigg {}prod _{lambda in Lambda }O_{lambda } {Bigg |} O_{lambda }in {mathcal {O}}_{lambda }}, 有限個のλを除いてOλ=Xλ}{displaystyle O_{lambda }=X_{lambda }{Bigg }}}
によって生成される位相と一致する。
Λが有限集合のときは、「有限個のλを除いて…」という条件がいらなくなるので簡単であるが、Λが無限集合のときは注意が必要である。
R1,R2,…{displaystyle mathbb {R} _{1},mathbb {R} _{2},ldots }



- ∏i∈NUi{displaystyle prod _{iin mathbb {N} }U_{i}}
は直積位相に関して
- ∏i∈NRi{displaystyle prod _{iin mathbb {N} }mathbb {R} _{i}}
の開集合ではない。実際、前述の「有限個を除いて…」という条件を満たしておらず、条件をみたすものの和集合としても書けないからである。
一方、直積位相よりも強い位相であるBox topologyでは、上述の集合は開集合となる。
像位相、商位相、終位相、直和位相
逆像位相、部分位相、始位相、直積位相と双対的に像位相、商位相、終位相、直和位相が定義できる。
像位相
(X,O){displaystyle (X,{mathcal {O}})}
- f:X→Y{displaystyle fcolon Xto Y}
を写像とする。このとき、
- f∗(O):={U⊂Y∣f−1(U)∈O}{displaystyle f_{*}({mathcal {O}}):={Usubset Ymid f^{-1}(U)in {mathcal {O}}}}
とすると、(Y,f∗(O)){displaystyle (Y,f_{*}({mathcal {O}}))}

次の事実が知られている
- 像位相は、写像 f: X → Y を連続とする最強の位相である
商位相
(X,O){displaystyle (X,{mathcal {O}})}

商写像
- π:X→X/∼,x↦[x]{displaystyle pi colon Xto X/{sim },;xmapsto [x]}
が商集合 X/∼{displaystyle X/{sim }}

終位相
像位相は以下のように一般化できる。
Y を集合とし、{(Xλ,Oλ)}λ∈Λ{displaystyle {(X_{lambda },{mathcal {O}}_{lambda })}_{lambda in Lambda }}
- fλ:Xλ→Y{displaystyle f_{lambda }colon X_{lambda }to Y}
を考える。
このとき、全ての {fλ}λ∈Λ{displaystyle {f_{lambda }}_{lambda in Lambda }}
終位相の開集合系は
- ⋂λ∈Λ(fλ)∗(Oλ){displaystyle bigcap _{lambda in Lambda }(f_{lambda })_{*}({mathcal {O}}_{lambda })}
と一致する。
直和位相
{(Xλ,Oλ)}λ∈Λ{displaystyle {(X_{lambda },{mathcal {O}}_{lambda })}_{lambda in Lambda }}


- ιλ:Xλ↪∐τ∈ΛXτ{displaystyle iota _{lambda }colon X_{lambda }hookrightarrow coprod _{tau in Lambda }X_{tau }}
の族 {ιλ}λ∈Λ{displaystyle {iota _{lambda }}_{lambda in Lambda }}

直和位相の開集合系は
- {⋃λ∈ΛOλ:Oλ∈Oλ}{displaystyle left{bigcup _{lambda in Lambda }O_{lambda }:O_{lambda }in {mathcal {O}}_{lambda }right}}
に一致する。
ヴィートリス位相、コンパクト開位相
ヴィートリス位相
(X,O){displaystyle (X,{mathcal {O}})}


- ⟨U1⋯Un⟩:={A∈F:A∩Ui≠∅(i=1⋯n),A⊆⋃i=1nUi}{displaystyle langle U_{1}cdots U_{n}rangle :={Ain {mathfrak {F}}:Acap U_{i}neq varnothing (i=1cdots n),Asubseteq bigcup _{i=1}^{n}U_{i}}}
と定義する(ただし F{displaystyle {mathfrak {F}}}




コンパクト開位相
(X,OX){displaystyle (X,{mathcal {O}}_{X})}






- W(K,O)={f∈C(X,Y)∣f(K)⊂O}{displaystyle W(K,O)={fin C(X,Y)mid f(K)subset O}}
とより定義する。
このとき {W(K, O) : K は X のコンパクト部分集合、O∈OY{displaystyle Oin {mathcal {O}}_{Y}}

基本近傍系
ユークリッド平面 R2 を位相空間と考え、その上に任意に固定した点 p を考える。p の近傍であるような R2 の部分集合は多種多様であるが、どのような近傍 V についても、十分に大きな正の整数 n を選べば、p を中心とする半径 1/n の開円板 B(p, 1/n) が V に含まれる。もちろんこの開円板は p の近傍である。以上から、開円板の族 {B(p,1/n) | n∈N}{displaystyle {B(p,1/n) | nin mathbf {N} }}
正確な定義は以下の通り。p が位相空間 X の点であるとき、p の近傍からなる族 U{displaystyle scriptstyle {mathcal {U}}}


もちろん、p が決まってもその基本近傍系は一通りには決まらない。たとえば上の例では、「p を中心として軸に平行な辺をもった一辺 1/n の開正方形全体」も基本近傍系である。また、p の近傍すべてからなる族も基本近傍系である。
位相の生成、開基、準開基
準開基
X を集合とし、S⊂P(X){displaystyle {mathcal {S}}subset {mathfrak {P}}(X)}
- ⋃S=X{displaystyle textstyle bigcup {mathcal {S}}=X}
このとき、
- S⊂O{displaystyle {mathcal {S}}subset {mathcal {O}}}
を満たす最弱な開集合系 O{displaystyle {mathcal {O}}}



なお、必要ならS{displaystyle textstyle {mathcal {S}}}

以上で我々は、準開基の抽象的な定義を与えたが、準開基の概念をより具体的な形で与えることもできる。
そのための準備として、まず準開基の関連概念である開基について学ぶ。
開基
(X,O){displaystyle (X,{mathcal {O}})}

以下が満たされるとき、B{displaystyle {mathcal {B}}}

O{displaystyle {mathcal {O}}}に属する任意の開集合(≠∅{displaystyle emptyset }
)はB{displaystyle {mathcal {B}}}
の元の(有限個または無限個の)和集合として書き表せる。
B{displaystyle {mathcal {B}}}

O{displaystyle {mathcal {O}}}に属する任意の開集合 O (≠∅{displaystyle emptyset }
)と任意の点 x ∈ O に対し、x∈Bx⊂O{displaystyle xin B_{x}subset O}
を満たす B{displaystyle {mathcal {B}}}
の要素 Bx{displaystyle B_{x}}
が存在する。
実際、この条件が満たされれば、
- O=⋃x∈OBx{displaystyle O=bigcup _{xin O}B_{x}}
と O を B{displaystyle {mathcal {B}}}
必要性の証明は省略。
開基の具体例
(X , d )を距離空間とし、O{displaystyle {mathcal {O}}}
- B={Br(x)∣x∈X,r>0}{displaystyle {mathcal {B}}={B_{r}(x)mid xin X,r>0}}
はO{displaystyle {mathcal {O}}}
実際、距離空間における開集合の定義より、O ⊂ X が開集合なら、
- ∀x∈O∃rx>0 : Brx(x)⊂O{displaystyle forall xin Oexists r_{x}>0~~:~~B_{r_{x}}(x)subset O}
なので、
O=⋃x∈O{displaystyle O=bigcup _{xin O}}Brx(x){displaystyle B_{r_{x}}(x)}
と O を B{displaystyle {mathcal {B}}}
開基の特徴づけ
X を集合とし、B⊂P(X){displaystyle {mathcal {B}}subset {mathfrak {P}}(X)}


このとき、B{displaystyle {mathcal {B}}}

- ⋃B=X{displaystyle bigcup {mathcal {B}}=X}
∀B1,B2∈B,∃B′⊂B{displaystyle forall B_{1},B_{2}in {mathcal {B}},exists {mathcal {B}}'subset {mathcal {B}}}: B1∩B2=⋃B′{displaystyle B_{1}cap B_{2}=bigcup {mathcal {B}}'}
準開基の特徴づけ
(X,O){displaystyle (X,{mathcal {O}})}

- ⋃S=X{displaystyle textstyle bigcup {mathcal {S}}=X}
を仮定する。
このとき、S{displaystyle {mathcal {S}}}


- B={⋂i=1nSi|n∈N,Si∈S}{displaystyle {mathcal {B}}=left{bigcap _{i=1}^{n}S_{i},{bigg |},nin mathbb {N} ,,S_{i}in {mathcal {S}}right}}
が、(X,O){displaystyle (X,{mathcal {O}})}
位相的性質
位相空間の定義それ自身は可能な限り一般的に定義されているため、個々の応用では位相空間にプラスアルファの性質を付け加えたものを考えることが多い。
本節では、そうしたプラスアルファの性質のうち代表的なものを紹介する。
分離公理
分離公理とは、位相空間 X 上の2つの対象(点や閉集合)を開集合により「分離」(separate)する事を示す一連の公理、もしくはそこから派生した公理である。
代表的な分離公理としてハウスドルフの分離公理があり、これは以下のような公理である:
X 上の相異なる2点 x、y に対し、x、y の開近傍 U、V があり、U∩V=∅{displaystyle Ucap V=emptyset }である。
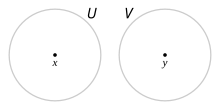
相異なる2点を分離するそれぞれの開近傍
ハウスドルフの分離公理は、点 x と y が開近傍という位相的な性質を利用して「区別」(separate) できる事を意味している。すなわちX の位相は点の区別が可能なほど細かい事をこの公理は要請している。
全ての位相空間がハウスドルフの分離公理を満たすわけではなく、例えば密着位相の入った空間には開集合は全体集合と空集合しかないのでこのような区別は不可能である。
一方、距離空間は必ずハウスドルフの分離公理を満たし、ハウスドルフの分離公理を満たす空間(ハウスドルフ空間)では点列の収束の一意性が成り立つことが知られている。
ハウスドルフ空間で点列の収束の一意性が成り立つのは、点列の収束先が x なのか y なのかが開集合により区別可能だからである。
このように分離公理は、位相空間上の対象を区別する上で重要な役割を担う。
| 位相空間 | 名前 |
|---|---|
| T0 | コルモゴロフ空間 |
| T1 | フレシェ空間(到達可能空間) |
| T2 | ハウスドルフ空間 |
T212{displaystyle T_{2{frac {1}{2}}}} | 完備ハウスドルフ空間、ウリゾーン空間 |
| T3 | 正則空間、正則ハウスドルフ空間 |
T312{displaystyle T_{3{frac {1}{2}}}} | チコノフ空間、完全正則空間 |
| T4 | 正規ハウスドルフ空間 |
| T5 | 全部分正規ハウスドルフ空間 |
| T6 | 完全正規ハウスドルフ空間 |
連結性
連結性とは、直観的には位相空間が「ひとつながりである」
という性質である。閉区間 [0,1] は連結性をもつ(連結である)が、二つの交わらない閉区間を合併した [0,1]∪[2,3]{displaystyle [0,1]cup [2,3]}![[0,1]cup [2,3]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f771855546506a8323bcf011a710de0927c631f0)
コンパクト性
位相空間 X のコンパクト性の概念はそれ自身は非常に抽象的で、X が「ハイネ・ボレルの被覆定理の結論部分」を満たすこととして定義される。
しかし X が(有限次元の)ユークリッド空間の部分空間であれば、コンパクト性は有界閉集合である事と同値である。
一般の距離空間の場合は、有界性より強い条件である「全有界性」という条件と「完備」とを両方満たすことと同値である。
有限次元のリーマン多様体の場合、有界性と全有界性に差はないが、無限次元の場合は両者に差がある。
ヒルベルト空間の(縁を含んだ)単位球は、有界かつ完備であるが全有界ではなく、従ってコンパクトでもない例となっている。
コンパクトな位相空間 X の最も重要な性質の一つは、以下の点列コンパクト性である
X 上の任意の点列は収束部分列を持つ
X が距離空間の場合は、コンパクト性と点列コンパクト性は同値である。
X が距離空間でない場合、両者は必ずしも同値でないが、「点列」の部分を「有向点族」に変えたものとは同値となる。
コンパクトでない空間、例えばR2{displaystyle mathbb {R} ^{2}}
例えば、コンパクトな距離空間上の実数値連続関数は必ず一様連続であるが、R2{displaystyle mathbb {R} ^{2}}
また、コンパクトな曲面は穴の数が有限であり、これを利用して曲面が位相的に分類されているが、コンパクトではない曲面は穴の数が無限に発散することもあり、より複雑である。
これらの例のように、コンパクトな空間は無限に関する複雑さを回避できるという利点がある。
可算公理と可分
位相空間X において可算公理は、X の位相的な対象(近傍系、開集合)が可算なものから生成されることを意味し、可算公理が成立する空間では、非可算特有の難しさを回避できる場合がある。
可分もこれと類似したモチベーションのもと定義される。
厳密な定義は以下の通りである
第一可算公理: X の任意の点 x に対し、x の近傍系は可算な基本近傍系を持つ
第二可算公理: X の開集合系は可算な開基を持つ
可分: X は稠密な可算部分集合を持つ
性質と例
以下が成立する:
- 第二可算公理を満たす⇒ 第一可算公理を満たし、かつ可分
- 距離空間⇒ 第一可算公理を満たす
しかし距離空間は第二可算公理を満たすとは限らない。
距離空間においては第二可算公理を満たす事と可分な事は同値である。
有限次元のユークリッド空間(あるいはより一般に多様体)は第二可算公理を満たす。(距離化可能なので可分でもある)。
一方、ユークリッド空間の「無限次元版」であるヒルベルト空間は距離空間であるが第二可算公理を満たすとは限らない。
しかし通常は第二可算公理を満たすヒルベルト空間のみを考えることが多く、そのようなヒルベルト空間は全て同型で、しかもそのようなヒルベルト空間にはベクトル空間としての可算基底が存在する事が知られている。
距離化可能性
距離空間は自然に位相空間になるが、では逆に位相空間がどのような条件を満たせば距離空間になるであろうか。
すなわち、位相空間 (X,O){displaystyle (X,{mathcal {O}})}

学部レベルの教科書には距離化可能性の十分条件であるウリゾーンの距離化可能定理が載っていることが多いが、現在は距離化可能性の必要十分条件である長田=スミルノフの距離化定理やビングの距離化定理が知られている。
この他の諸性質
一般の位相空間についても、連続性や収束を大枠において論じることができる。しかし、当然のことながら、ユークリッド空間がもつような「都合のよい」性質がすべての位相空間で成り立つ訳ではない。個々の位相空間を取り扱うには、その位相空間がどのような点でユークリッド空間に類似し、どのような点が違うのかを明確に知っておくことが重要である。
位相空間についての性質は、上に挙げたコンパクト性、連結性などの他にも色々考えられるが、よく用いられるものの多くはユークリッド空間について成り立つ性質の一つを取り出してきたものである。このような性質の有無を知ることにより、どのような議論がユークリッド空間と並行してできるのかを識別できる。例えば局所コンパクト性とは、各点がコンパクトな近傍をもつという性質であるが、これはユークリッド空間について成り立つ性質の一つである。しかし、この性質は整数論で用いられるp-進数体 Qp についても成立する。一方、有理数全体 Q は局所コンパクトではない。
ユークリッド空間については成立しない性質の中にも注目に値するものがあり、時として利用される。たとえば、連結な部分空間が一点に限られる空間を完全不連結というが、これはユークリッド空間にはない性質である。Q はこの性質を満たすし、また p-進数体 Qp もこの性質を満たす。
発展的なトピック
連続体論
連続体(れんぞくたい、英: continuum)とは、空でないコンパクト連結距離空間、あるいはより一般にコンパクト連結ハウスドルフ空間のことを言う。
ユークリッド空間上の閉曲面は連続体となるが、連続体論ではこのような「常識的な」空間に留まらず幅広く連続体一般を研究する。
具体的にはヒルベルト空間の無限次元部分集合であるにもかかわらずコンパクトな ヒルベルト立方体
∏n∈N[0,1/n]{displaystyle prod _{nin mathbb {N} }[0,1/n]}、
フラクタル図形のシェルピンスキーのカーペット、ホモトピー群は自明となるが可縮空間ではないワルシャワの円などが研究対象となる。

ワルシャワの円
完全不連結性とカントール空間
学部レベルの位相空間論で登場する概念の多くは、曲面のような「常識的な」空間における性質を抽象したものである。
しかし完全不連結性はこうした範疇から外れた性質で、位相空間 X 上の連結部分集合は空集合、全体集合、および一点集合に限られる事を意味する。
完全不連結な空間の例としては有理数の集合Q{displaystyle mathbb {Q} }
しかし完全不連結な空間はQ{displaystyle mathbb {Q} }
カントール集合(に実数体から誘導される距離をいれたもの)は、完備距離空間でありながら完全不連結な空間の例となっている。
実はカントール集合はこのような空間の典型例の一つであり、以下の性質を満たす空間(カントール空間)は必ずカントール集合と位相同型になることが知られている(ブラウワーの定理):
- 孤立点を持たない非空の完全不連結コンパクト距離化可能空間
ベール空間
位相空間X がベール空間であるとは、X 上の稠密開集合の可算個の共通部分が必ず稠密になることを言う。
完備疑距離空間の開集合はベール空間になる(ベールの第一範疇定理)。
また局所コンパクトハウスドルフ空間もベール空間になる(ベールの第二範疇定理)。
ベールの範疇定理は関数解析学において、開写像定理や閉グラフ定理を証明するのに用いられる。
集合論的位相空間論
集合論的位相空間論とは、位相空間上の性質がZFCと独立かどうかを主題する分野である。
位相ゲーム
位相ゲームとは、2人のプレイヤーにより位相空間上で行われるゲームで、プレイヤー達が自分の手番のとき、何らかの位相的な対象(開集合や閉集合など)を指定する事でゲームが進んでいく。
位相空間上の様々な性質、例えばベールの性質が位相ゲームのゲーム理論的な性質と関連する(バナッハ・マズール・ゲーム)。他にも完備性、収束性、分離公理といったものもゲーム理論的な性質と関連する。
位相代数的構造
代数的な演算が定義された位相空間X は、その演算の作用がX 上連続になるとき、演算と位相は両立するという。
そのような例として代表的なものには位相群、位相環および位相体、位相線型空間などがある。
位相順序構造
スペクトル空間: 位相空間がスペクトル的となるための必要十分条件は、それが何らかの環の素スペクトルとなっていることである。- 標準順序: 位相空間の特殊化前順序または標準前順序は、x≤y⇔Cl({x})⊆Cl({y}){displaystyle xleq yLeftrightarrow operatorname {Cl} ({x})subseteq operatorname {Cl} ({y})}
で定義される。
歴史
集合論の創始者ゲオルク・カントールはユークリッド空間の開集合や閉集合などについても研究したが、これが位相空間の研究のはじまりである。カントールの行ったような位相空間の古典的な研究は、点集合論と呼ばれる。その後、モーリス・フレシェはユークリッド空間から離れて距離空間において極限の概念を考察し、さらにその後フェーリクス・ハウスドルフ、カジミェシュ・クラトフスキらによって、次第に現代のような一般の位相空間の形に整えられていった。
参考文献
出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。記事の信頼性向上にご協力をお願いいたします。(2016年2月) |
- Armstrong, M. A.; Basic Topology, Springer; 1st edition (May 1, 1997). ISBN 0-387-90839-0.
- Bredon, Glen E., Topology and Geometry (Graduate Texts in Mathematics), Springer; 1st edition (October 17, 1997). ISBN 0-387-97926-3.
Bourbaki, Nicolas; Elements of Mathematics: General Topology, Addison-Wesley (1966)..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
OCLC 221789308
Čech, Eduard; Point Sets, Academic Press (1969).
OCLC 10256
Fulton, William, Algebraic Topology, (Graduate Texts in Mathematics), Springer; 1st edition (September 5, 1997). ISBN 0-387-94327-7.- Lipschutz, Seymour; Schaum's Outline of General Topology, McGraw-Hill; 1st edition (June 1, 1968). ISBN 0-07-037988-2.
Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.- Runde, Volker; A Taste of Topology (Universitext), Springer; 1st edition (July 6, 2005). ISBN 0-387-25790-X.
Steen, Lynn A. and Seebach, J. Arthur Jr.; Counterexamples in Topology, Holt, Rinehart and Winston (1970). ISBN 0-03-079485-4.
Willard, Stephen (2004). General Topology. Dover Publications. ISBN 0-486-43479-6.
- 松坂, 和夫 『集合・位相入門』 岩波書店、1968年。
ISBN 4-00-005424-4。
脚注
^ 2.からは空積は出てこず、1.無しには開集合全体の合併が空間全体になるとは言えない。実際{{},{x}}は空間{x,y}において規約の元 2.、3. を満たすが位相にはならない。
関連項目
- 空間 (数学)
- ポイントレス位相空間論
- 位相幾何学
- 関数解析学
- 距離空間
外部リンク
- Weisstein, Eric W. "topological space". MathWorld(英語).
topological space - PlanetMath.(英語)
酒井克郎. “位相空間の基礎概念 (PDF)”. 2011年11月閲覧。(2008年度 筑波大学 トポロジーI 講義用レジュメ)
位相空間 - J-GLOBAL
- 日本大百科全書(ニッポニカ)『位相空間』 - コトバンク

























![{displaystyle (a,infty ]={xin mathbb {N} mid x>a}cup {infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610104f573d907feb2c0bfd5cc1c5a299cd8297d)















![{displaystyle pi colon Xto X/{sim },;xmapsto [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037582838a856306383d0a9769bb5c25797ee154)












